複素数は慣れが肝心！簡単な座標計算をしてみましょう

こんにちは、ゆうぞうです。

今回は関数電卓の複素数モードで、
トラバー点からの観測結果を使って筆界点を算出し、土地の地積を求めるまでを計算してみましょう。

電卓の操作方法については私がオススメするCANON F-789SGを使用するものとして話を進めていきますね。

 

過去記事⇒複素数計算に便利すぎる。土地家屋調査士試験に使う電卓はキャノンF-789SGで決まり！

計算前に関数電卓の設定をしましょう

関数電卓は購入したばかりの初期設定だと、小数点が分数で表示されたりとストレスの溜まる設定になっています。

また、複素数モードへの切り替えも必要になってきますので、

計算を行う前に必ず設定を変更し土地家屋調査士試験に適した状態にしておくことが必須となります。

Lineモードに切り替えます

これで分数で表示されなくなりました。

CPLXモード(複素数モード)に切り替えます

これで複素数モードに切り替わりました。

複素数計算を行うとき、
例えば座標A(X:10.00,Y:10.00)があったとします。この場合は、
Xを実数（10.00）
Yを虚数（10.00 i ）
で表示します。

初めは何となく違和感を感じるかもしれませんが、それもすぐに慣れます。
初めの内はY座標の最後に「 i 」を付け忘れることが多いので気をつけましょう。

小数点以下の表示設定をします

土地家屋調査士試験では例年、

小数点第２までの解答を求めています。

これは個人の好き嫌いもありますが、「Fix」を使用することで小数点以下の表示を任意で変更することが出来ます。

これで小数点以下第２位までの表示になりました。
ちなみにこの場合、小数点以下第３位は四捨五入されます。

しかし、今回は実務に合わせて小数点以下第３位の問題を作りましたので、STEP３の数字は３にして下さい。

問題を確認しましょう

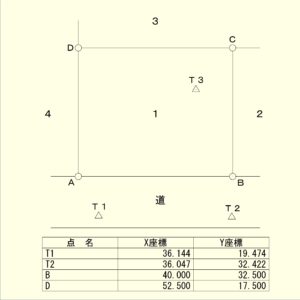
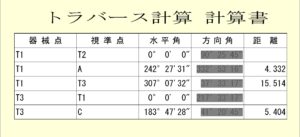
※上記画像をクリックすると拡大で確認出来ます。

土地家屋調査士試験では小数点第２位までの計算ですが、
今回は実務に合わせて小数点第３位までの数値で計算することにします。

また、計算された座標値は小数点第４位を四捨五入したものを使用します。

計算前の下準備をします

今回の問題では筆界点B、Dおよびトラバー点T１、T２の座標値が与えられていますので、

既知点を関数電卓にメモリーしていきますが、

まずはB（４０．０００，３２．５００i）を「メモリーB」に保存してみましょう。

他の既知点座標も同様の方法でメモリーしてみて下さい。

メモリーする際にはどこに保存したか忘れないように、
問題用紙にメモを残したり、普段から筆界点はA〜F、X、Y、Mに保存するなどの自分ルールを作っておくと忘れないですし、試験本番でも慌てずに済むので良いですね。

複素数を使ってトラバーT３と筆界点Aを計算します

トラバーT１点から観測点を計算するときは、

T１＋距離∠方向角

が関数電卓での基本的な公式になります。

注意点としては観測水平角では無いということです。

 

まずはT１から筆界点Aの方向角の求めます。

 

ここで求めた方向角は「メモリー０」等に保存しておくと後で使用するので便利です。

次に筆界点座標Aを求めます。

これで筆界点Aの座標値が求まり、「メモリーA」に保存されました。

 

これと同様にしてトラバーT３を求めると、

T３「４８．４４３＋２８．９３０i」

と計算できますので、これは「メモリー３」に保存してください。

複素数を使って筆界点Cを計算します

基本的には先程の筆界点Aを求めた方法と同様の作業となります。

まずはT３から筆界点Cの方向角を求めます。

次に筆界点座標Cを求めます。

これで筆界点Cの座標値が求まり、「メモリーC」に保存されました。

以上で筆界点A、B、C、Dの座標値が求まり、

それぞれ「メモリーA」「メモリーB」「メモリーC」「メモリーD」に保存することができました。

複素数を使って地積を求積します

筆界点座標全てが明らかになりましたので、それぞれの座標値から地積を算出します。

最後に

いかがだったでしょうか。

複素数を使いこなしている方には物足りなかったと思いますが、
まだ使い慣れていない方にとっては、このような計算問題で基本操作を覚えていくことが大切です。

 

土地家屋調査士試験で実際に使用する複素数モードのテクニックはさほど多くはありませんので、
同じ問題を同じ方法で反復することで体が操作法を覚え、問題を読み込んでいく中どのような解法を用いていくか自然と出てくるようになります。

 

実際の測量と一緒で

見るより慣れろ

ということですね。

 

実際の業務でも思うことですが、
頭であれこれ考えるよりもまずは行動して体感することが大切です。

もちろん深くまで考えを廻らせ考察することも大切ですが、あまり熱中しすぎても時間を浪費するだけで終わるケースもあります。

ですので、始めは全体像を掴むまで「慣れ」ることを目指しましょう。

「慣れ」ると意外と関連事項の知識や理解が深まり、自分の中で腹落ちするものですよ。

 

それではまた。

最後までお読みいただきありがとうございます。

スポンサーリンク

スポンサーリンク