こんにちは、ゆうぞうです。
久しぶりに関数電卓使用法について解説していきたいと思います。
今回は隅切り計算についてです。
よくあるケースを想定して問題を作りました。複素数を使用して計算しますので、関数電卓の練習問題にいかがでしょうか。
電卓の操作方法については私がオススメするCANON F-789SGを使用するものとして話を進めていきます。
Contents
例題の確認
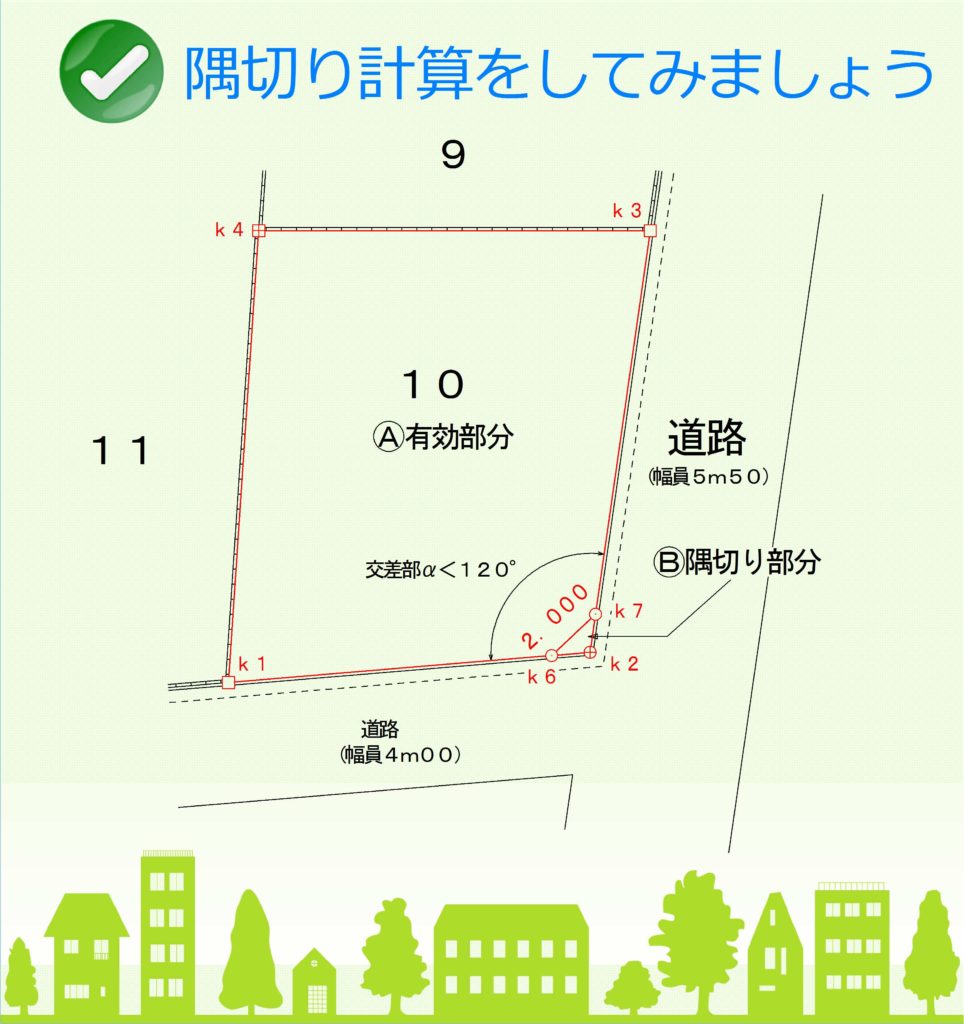
事案の確認
１０番土地所有者が住宅を新築しようと計画したところ、接道する２面の道路がどちらも幅員６m未満で道路の交差部も角度１２０°未満のため、角地による建築制限がかかると指導を受けました。行政の指導より底辺２mの二等辺三角形で隅切りを設け、宅地部分と隅切り部分を分筆することになりました。
※角地による隅切りの取り扱いについては自治体ごとで異なるため、底辺２mを指導する地域もあれば１辺を２mとする地域もあり実務上はその都度確認する必要があります。基本的には接道する道路幅員と交差部の角度により隅切りの有無が決まるケースがほとんどです。
【例題】
【既知点座標】
| 測点名 | X座標 | Y座標 |
| k1 | 3.000 | 3.000 |
| k2 | 4.000 | 15.000 |
| k3 | 18.000 | 17.000 |
| k4 | 18.000 | 4.000 |
| k6 | ||
| k7 |
今回は筆界点座標は全て既知点というケースで、隅切り点k6、k7を求めていきます。
計算前に「二等辺三角形」の特徴をおさらい
どうして今更二等辺三角形の定理やその性質をおさらいする必要があるのか。
それは二等辺三角形の隅切りを計算する問題は、二等辺三角形の性質を利用して求めるケースが非常に多いからです。
例えば、隅切りの頂角を二等分する性質を利用して角度を求め、三角関数で更に辺長を求めたりするなどです。
つまり隅切り計算する上で念頭に置くのは図形の性質です。とても大事なことですので、ここでしっかり押さえておきましょう。
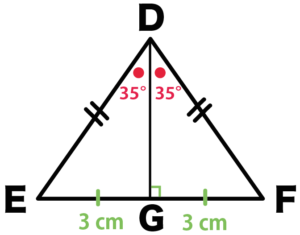
二等辺三角形
定理
「２つの辺が等しい三角形」
性質
「２つの底角は等しい」
「頂角の二等分線は、底辺を垂直に2等分する」←これよく使います。
ではさっそく複素数モードで計算してきましょう
まずは既知点をメモリーに登録しましょう
今回はk1、k2、k3、k4が既知点ですので、全て電卓にメモリーしましょう。
操作方法
３．０００＋３．０００iShift RCL（STO）＋( – )（A）
RCL ( – )
画面に「３．０００＋３．０００i」が出れば無事完了です。
※Ｙ座標の最後に虚数「i」の付け忘れにご注意下さい。
これでメモリーAに筆界点k１が登録されました。
同様にk2、k3、k4をメモリーB、Ｃ、Ｄに登録してください。
交差部の角度があやしい。角度を求めてみよう。
繰り返しになりますが、隅切り計算ではまず疑うのは二等辺三角形の性質です。
今回は底辺2ｍ00の条件がありますから何となく、
「頂角の二等分線は、底辺を垂直に2等分する」
が使えそうな気がします。
ですので、初めに∠k1k2k3の角度を求めたいと思います。
角度の求め方ですが、△k1k2k3について全て座標値がわかっていますので方向角の差から角度をだしていきます。
イメージはこんな感じです。
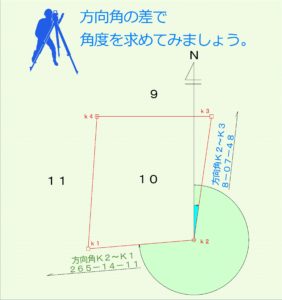
では関数電卓で計算していきましょう。
A点⇒B点の方向角
Arg(B-A)=方向角
操作方法
Apps３(Arg)RCL( – )(A) – RCL(° ′ ″)（B） + 360°＝２６５°１４′１０．８９″（k2～k1の方向角）
※求めたい方向角の先の点（Ｋ1）から元の点（Ｋ2）を引きます。（うまく言葉で表現できない・・・）
※求めた数値がマイナスの角度になった場合のみ３６０°を足して下さい。
Apps３(Arg)RCLhyp(C) – RCL(° ′ ″)（B）＝８°７′４８．３７″（k2～k3の方向角）
（k1～k2の方向角） － （k1～k2の方向角）＝２５７°６′２２．５２″となります。
よって、３６０° － ２５７°６′２２．５２″＝１０２°５３′３７．４８″（∠k1k2k3となります。)
✅ この手法は土地家屋調査士試験では多用しますので、馴れておきましょう。
二等辺三角形の性質を応用してK2～K6、K2～K7の辺長を計算しましょう
イメージしましょう。
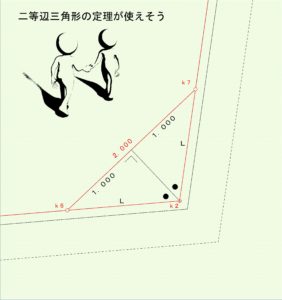
ピンときましたか？
そうです。三角関数の「Sin」を使えば、k2〜k6辺長とk2〜k7辺長が求められそうです。
k2〜k6辺長から求めていきましょう。
Sin●＝１m０００➗L（k2〜k6）の式が成り立つので、
L（k2〜k6）＝１m０００➗Sin●です。
●の角度は１０２°５３′３７．４８″の半分ですので５１°２６′４８.７４″となります。したがって、
L（k2〜k6）＝１２７８７２２・・・・・となります。
距離と方向角が分かれば後は楽勝です
Ｋ2からの距離と方向角が分かれば後は楽勝で座標値を求めることが出来ます。
ｋ2点はメモリーBに保存したと仮定
B+距離∠方向角=求点
操作方法
RCL(° ′ ″)（B）+1.2787∠（ Apps３(Arg)RCL( – )(A) – RCL(° ′ ″)（B） ) + 360° )
３．８９３８
１３．７２５７ⅰ
と表示されていればＯＫです。
よって、ｋ6座標は【Ｘ ： ３．８９４ , Ｙ : １３．７２６】となります。
同様の操作でｋ7も求めます。操作法は割愛しますが、結果として
ｋ7座標は【Ｘ ： ５．２６６ , Ｙ : １５．１８１】となります。
ついでに全体の面積を計算してみましょう
四角形ABCDの面積
Conjg(A)B+Conjg(B)C+Conjg(C)D+Conjg(D)A=倍面積
倍面積÷２＝面積（地積㎡）
Apps４(Conjg)RCL( – )(A) ) RCL(° ′ ″)（B） + Apps４(Conjg)RCL(° ′ ″)（B） ) RCLhyp（C） + Apps４(Conjg)RCLhyp(C) ) RCLsin（D） + Apps４(Conjg)RCLsin(D) ) RCL( – )（A） = 倍面積
８４２．０００
－３６１．０００ⅰ（虚数部分が面積となります）
これを２で割った数値が地積となります。
よって、四角形k1k2k3k4の地積は【 １８０．５０㎡ 】となります。
宅地有効部分と隅切り部分の面積については、同様の方法で求めることが出来ますので、興味のある方はチャレンジしてみて下さい。
最後に
長々と書きなぐりましたが、慣れればあっという間に解けるようになります。
基本操作を体が覚えるまで叩き込めば、よっぽどのことがなければ忘れません。電卓の操作練習であれば暇な時間にちょいちょいとできますし、勉強離れしてきた方は特に今一度、操作方法の確認をしてみるのはいかがでしょうか。
ゆうぞうさま はじめまして。
いち受験生です。
僕も同様の電卓を使用しております。いくつか計算方法があるとは思うのですが、“４点交点”はどのように操作されておりましたでしょうか？
差し支えなければご教授願います。
まこと様コメントを頂戴し有難うございます。
「CANON F-789SG」使いやすいですよね。
さて4点交点ですが、計算方法として
1、手計算
2、複素数（関数電卓のモード）
3、EQN（関数電卓のモード）
があります。
その内でも私は「EQN」で計算しておりました。
理由は単純に慣れていたからなのですが、計算スピードだけで言えば複素数の方が早いと思います。
自分がよりミスの少ない計算方法が最善かと思います。
ちなみに私は関数電卓２台のうち1台は複素数専用、もう1台は通常計算とEQN計算に使用していました。