実務向け、線上点が正しく座標計算出来ていたか関数電卓でチェックしてみた。

こんにちは、ゆうぞうです。

 

実務では筆界の区画計算をおこなう時、道路境界を考慮する上でその土地の街区を測量し、街区全体を検討することがあります。

 

その場合街区に曲がりがなければ、端から端を結ぶ直線上に当該地と道路との筆界点を計算します。

通常ブルートレンドやインフィニティー等のCADソフトを使用して交点計算や線上チェックをおこないますので、関数電卓による手計算は出来なくてもあまり問題ではありませんが、市役所等と打ち合せの際に「この検討図の仮点ちゃんと街区線上にのってる？」と聞かれた場合に即座に計算出来たら便利かなと思います。

 

今回は「打ち合せ」や「急に計算点に不安を覚えた時」に対応できるよう、
関数電卓の複素数モードを使用して、
既知点（街区座標点）の線上に当該地の計算点がちゃんと計算されているか関数電卓を使用してチェック計算してみましょう。

 

電卓の操作方法については私がオススメするCANON F-789SGを使用するものとして話を進めていきます。

計算前に関数電卓の設定をしましょう

過去記事で「CPLXモード(複素数モード)」の切り替えについてはご紹介しておりますので、そちらをご参考ください。

 

また、過去記事では「Fix」を小数点第３位の表示に設定しましたが、今回は線上チェックですので0.1ミリの単位まで確認したいので小数点第４位の表示に切り替えたいと思います。

小数点以下の表示を第４までに切り替えます

「Fix」の機能を使用して小数点第５位を四捨五入して下４桁表示にしたいと思います。

これで表示が切り替わりました。

例題の確認

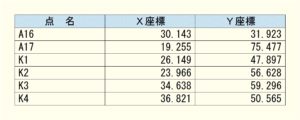
今回は上記の街区の「K１」が「A１６」と「A１７」の線上にちゃんと計算出来ているかチェックしていこうと思います。

どうなると直線上なのかの判断ですが、
△A１６K１A１７と仮定した時に高さ「h」が0,000以下の数値が出れば線上であると判断します。

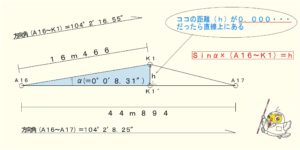
上記の図でほぼ答えが出たようなものですが、丁寧に次から計算していきます。

複素数モードで計算しよう

あくまでチェック計算ですので全て既知点です。

その上で△A１６K１A１７の高さ「h」を求めるには次の２項目を計算することで算出します。

 

 

上記の数値を使用して高さ「h」を求めるわけですが、これは三角関数の正弦定理の公式を使用して割り出します。

 

 

では、一つずつ計算していきます。

まずは使用する既知点をメモリーに登録しよう

今回はA１６とA１７とK１を使用してチェック計算しようと思いますので、この３座標をメモリーしてください。

 

 

これでメモリーAに筆界点A１６が登録されました。

同様にA１７をメモリーBにK１をメモリーCに登録してください。

①　A１６〜K１の点間距離の計算

 

②　角α（∠A１６ K１ A１７）

角αの求め方は方向角の差を利用して求めます。

これは土地の書式問題ではよく使われる一般的な解法なのでご参考ください。

 

 

高さhを算出しましょう

上記で計算した数値を下記の公式に当てはめてみましょう。

 

 

これで、線上チェックが出来ました。

結果は０．７ミリの高さということで線上にちゃんと計算出来ていたことがわかったわけですね。

最後に

土地家屋調査士試験おいてこの線上チェックをすることはありませんが、実務上こういう知識があっても良さそうなのでご紹介させて頂きました。

 

文章にすると長文になり面倒くさく感じますが、実は電卓を打って「h」の数値を出すまで１〜２分程の作業です。
これなら「打ち合せ中」でも「電車の中で座りながら」でもパパッと確認できますよね。

 

覚えておいて得するかと言われると分かりませんが、損はしないはず。
気になった方は是非お試し下さい。

「スキマ時間で択一問題」のカテゴリで

受験生皆様の電車通勤、お昼時間、就寝前の15分などの

スキマ時間の有効活用にちょうど良い択一問題を配信しています。

お手隙の時間にご活用下さい。

最後までお読みいただきありがとうございます。

それでは、また。

にほんブログ村

スポンサーリンク

スポンサーリンク